Abstract

Posing high-contact interactions is challenging and time-consuming, with hand-object interactions being especially difficult due to the large number of degrees of freedom (DOF) of the hand and the fact that humans are experts at judging hand poses. This paper addresses this challenge by elevating contact areas to first-class primitives. We provide end-to-end art-directable (EAD) tools to model interactions based on contact areas, directly manipulate contact areas, and compute corresponding poses automatically. To make these operations intuitive and fast, we present a novel axis-based contact model that supports real-time approximately isometry-preserving operations on triangulated surfaces, permits movement between surfaces, and is both robust and scalable to large areas. We show that use of our contact model facilitates high quality posing even for unconstrained, high-DOF custom rigs intended for traditional keyframe-based animation pipelines.We additionally evaluate our approach with comparisons to prior art, ablation studies, user studies, qualitative assessments, and extensions to full-body interaction.

What is this paper about?

We developed an easy way to create poses involving contact between objects. We do this by having users directly manipulate the contact areas between objects, rather than tediously pose each object keyframe-by-keyframe as in traditional workflows. Once the user has specified the desired contact areas, an inverse kinematics (IK) optimization automatically solves for the pose. We additionally developed a suite of artist tools that allows users to intuitively and accurately manipulate areas of contact directly on surface meshes, at interactive rates.

Central to our method is our contact model. Areas of contact ("patches") are specified by selecting an area on a surface mesh. The user then draws any curve(s) they like to act as a "handle" with which to control the patch. We call this curve (or set of curves) the axis. Typically, users choose some longitudinal or skeleton-like curve to act as the axis. In the screenshot below, axes for various contact patches on the hand are shown in purple. The axis is what allows us parameterize the patch — and users to manipulate the patch — accurately and efficiently.

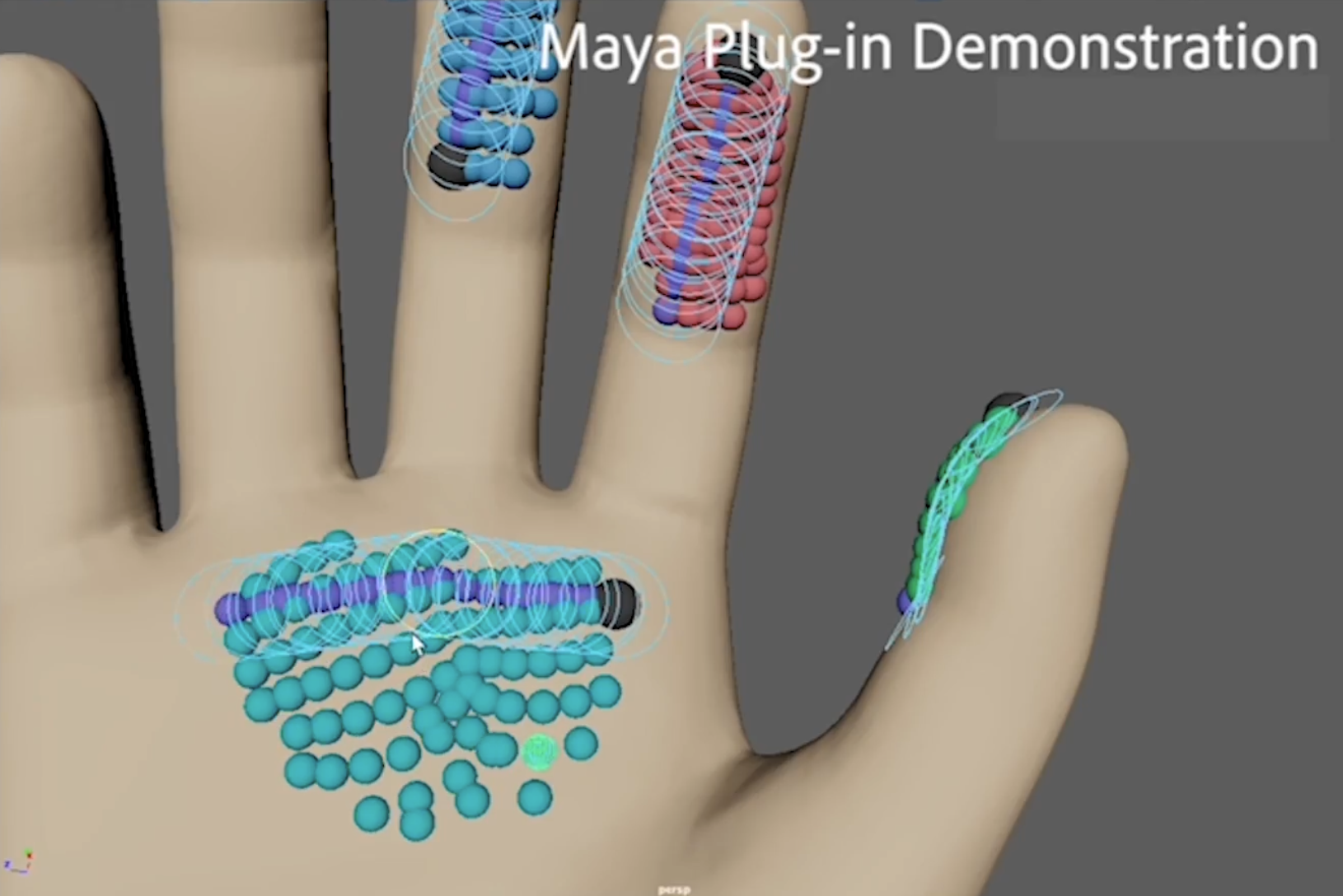
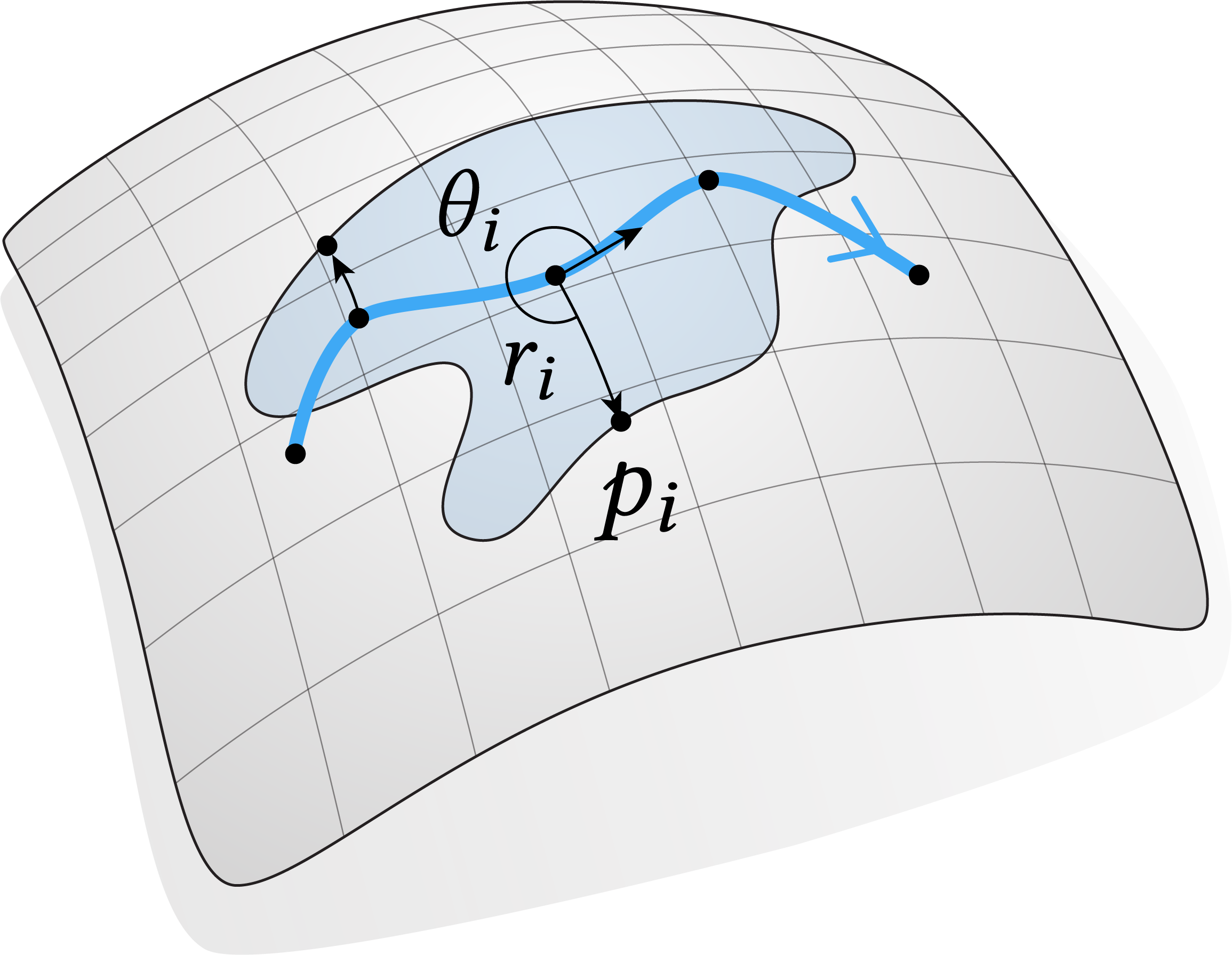
In a single pre-computation step, our method parameterizes the patch with respect to the user-drawn axis. Specifically, we represent each point of the patch using coordinates given by the logarithmic map with respect to its closest point on the axis. Intuitively, if \(p\) is a point in the patch, and \(q\) the closest point on the axis, then \(\log_q p\) gives the direction \(\theta\) and distance \(r\) one must walk starting from \(q\) to get to \(p\) (diagram below.) (Differential geometers may recognize this idea in connection to geodesic normal coordinates.) In words, the patch is entirely determined by lengths and angles with respect to the axis.

The log map gives us a local parameterization of the patch that is simple to compute. The patch's position is then completely determined by its axis and parameterization with respect to the axis, meaning that one can manipulate a patch simply by manipulating its axis. For example, one can change the wrap of a tentacle simply by changing the starting direction of the axis (below, left). In contrast, manually posing the tentacle for each grasp would be very tedious!

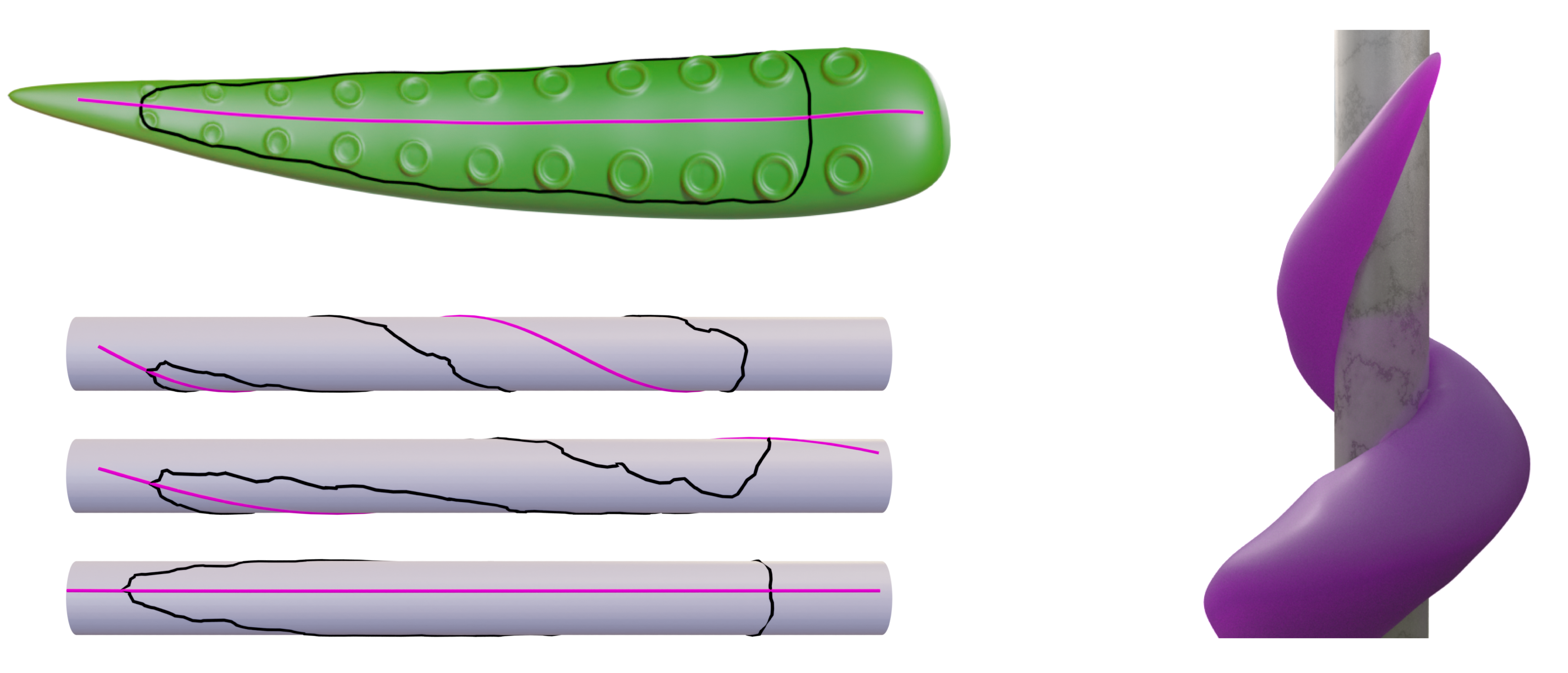
Once the parameterization has been computed — which only needs to be done once — a patch can be reconstructed at any time by tracing geodesics of fixed lengths and directions, which simply amounts to a sequence of arithmetic operations. Super fast and efficient!

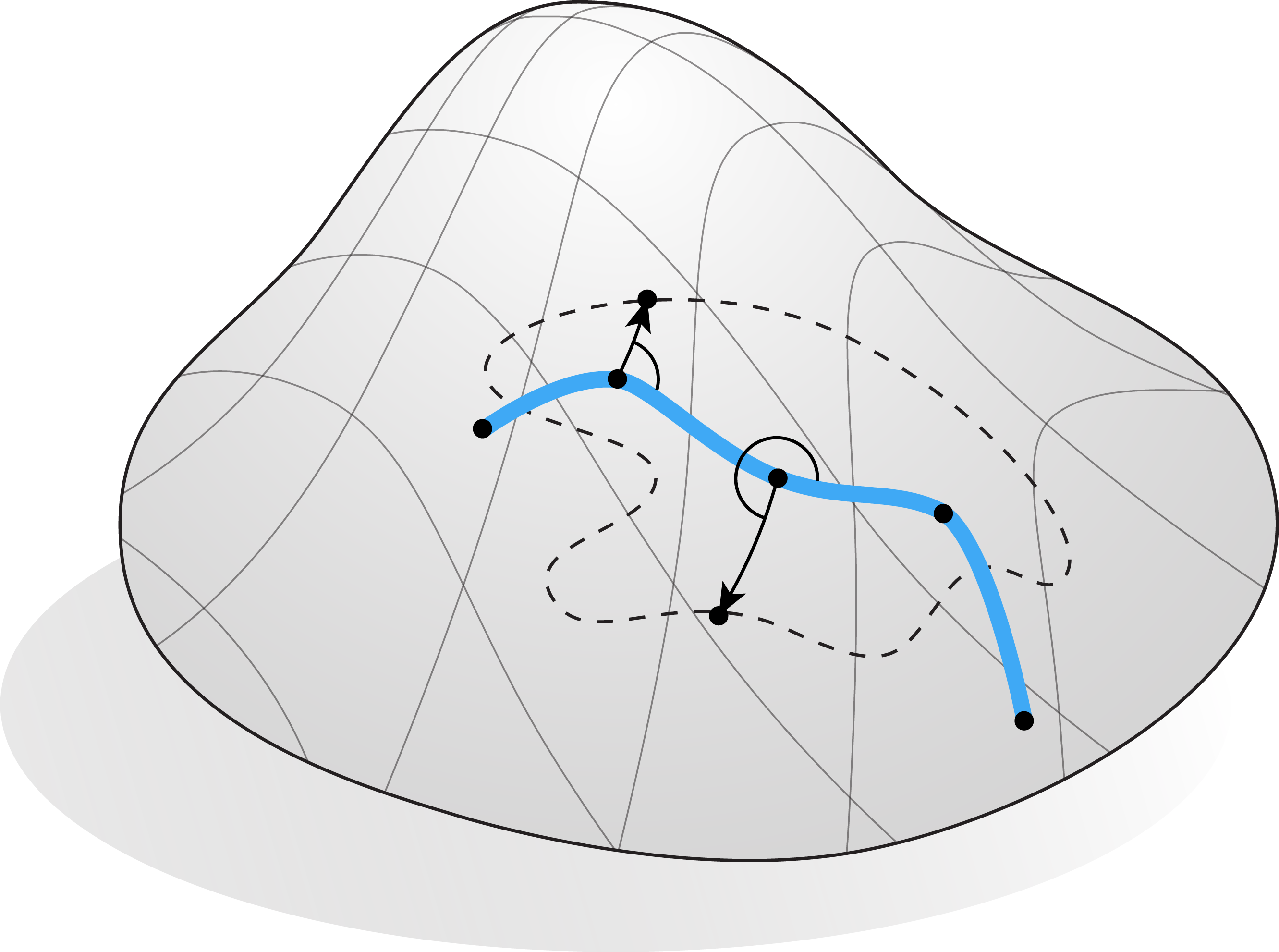
The axis itself is also determined entirely by the lengths and (relative) angles of its constituent segments. In fact, the only degrees of freedom are the position and direction of a single one of its segments — in particular, once one point \(q\) on the axis has been fixed, the rest of the axis is completely determined up to a global rotation about \(q\). These two degrees of freedom are precisely what we need to define all our patch manipulation operations.

In particular, rotating a patch simply amounts to rotating the axis; and rotating the axis simply amounts to choosing an initial direction for one of its segments, while keeping the rest of the axis rigid. One can also locally deform a patch by rotating only a part of the axis; this is done by simply changing the relative angle between two segments (while keeping the rest of the axis rigid.) One can translate a patch along a path on the surface mesh by performing parallel transport of the axis along the path, which again simply amounts to a sequence of arithmetic operations.

These patch operations essentially form the equivalent of a standard 2D graphics editor, but on surfaces. Using our method, you can rotate or click-and-drag patches across a surface mesh in real time, just like you would flat 2D graphics in the plane. One can also transfer a patch on one surface \(M\) to a different surface \(M'\) by simply specifying a starting position and direction for the axis on \(M'\), where the patch is reconstructed using the aforementioned tracing procedure.

Our contact model allows any point on the surface to be used as an axis or contact point, although the Maya plug-in only allows vertex selection due to Maya's user interface.

In this paper, we focused on hand-object interactions, which form an important class of contact-rich interactions. But our method can be used to model contacts between other types of objects, like between a body and a chair:

There could be some extensions that would make our method even more powerful. For example, how should we model more dynamic grasps, where objects may be changing in time? Currently we must re-parameterize the patch if the patch changes, or the underlying surface deforms very non-isometrically, which may be inefficient in dynamic animations. Second, a log map-based parameterization will exhibit large distortion if the source and target areas of the surface mesh differ dramatically in curvature — how can we better model patches on surfaces with large variations in curvature? These are all open questions for future work.