Solvers

There are two solvers: SignedHeatTetSolver solves for SDFs on a tetrahedralized domain, and SignedHeatGridSolver solves for SDFs on gridded domain. Both solvers assume the domain is rectangular, though future releases may consider arbitrary domains.

SignedHeatTetSolver(verbose: bool = True)

Construct an SDF solver that acts on a tet-meshed domain.

• verbose: If True, print status updates during solves.

SignedHeatGridSolver(verbose: bool = True)

Construct an SDF solver that acts on a gridded domain.

• verbose: If True, print status updates during solves.

To improve performance, operators and spatial discretizations are only built as necessary, and re-used in future computations if the underlying discretization hasn’t changed. This means future computations can be significantly faster than the initial solve (which includes, for example, tet mesh construction and matrix factorization.)

Signed distance to triangle and polygon meshes

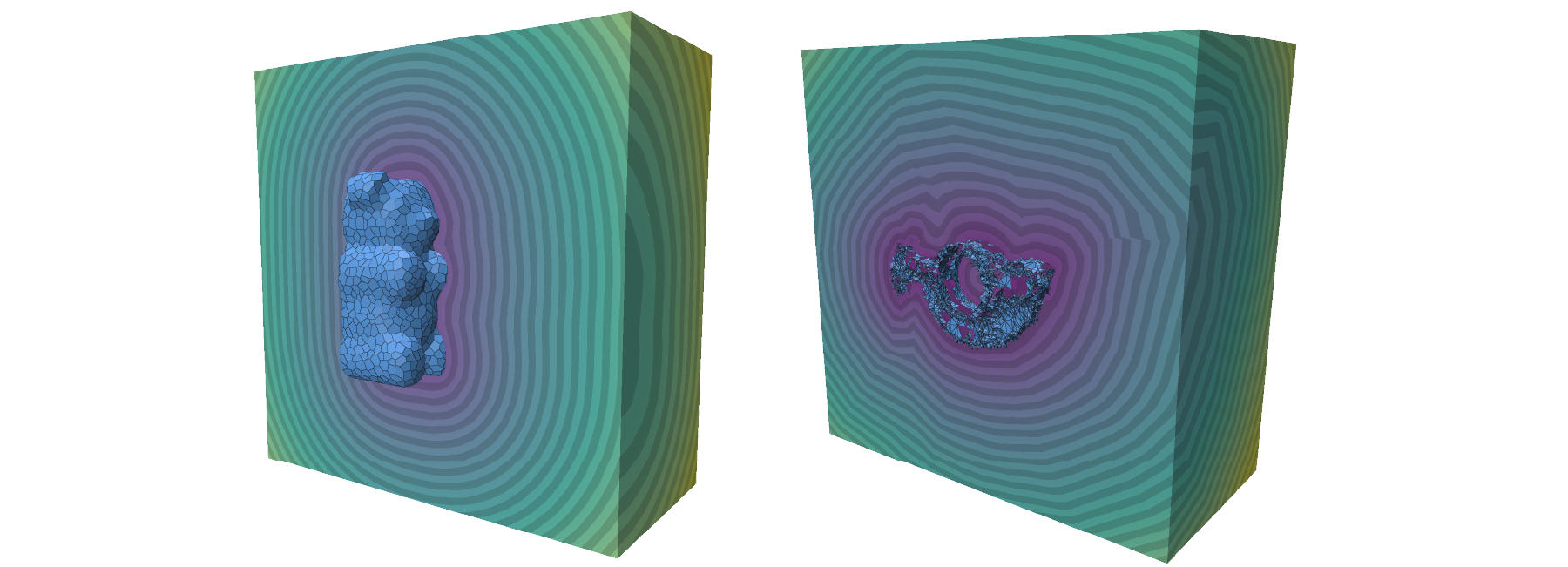
Example:

import signedheat3d as shm

V, F = # your mesh

# Initalize tet mesh solver
tet_solver = shm.SignedHeatTetSolver(verbose=True) # print all messages

# Solve!
sdf_tets = tet_solver.compute_distance_to_mesh(V, F)

# Solve on a regular grid instead.
grid_solver = shm.SignedHeatGridSolver(verbose=True)
sdf_grid = grid_solver.compute_distance_to_mesh(V, F)

SignedHeatTetSolver.compute_distance_to_mesh(V: np.ndarray, F: list[list[int]], options: dict = {}) -> np.ndarray

Solve for an SDF on a tet mesh, to the mesh represented by the vertex array V and face array F.

• V is a (n_vertices, 3) NumPy array of 3D vertex positions, where the i-th row gives the 3D position of the i-th vertex.
• F is a list of lists; each sublist represents a polygonal mesh face of arbitrary degree, using 0-indexed vertices.

SignedHeatGridSolver.compute_distance_to_mesh(V: np.ndarray, F: list[list[int]], options: dict = {}) -> np.ndarray

Solve for an SDF on a grid, to the mesh represented by the vertex array V and face array F.

• V is a (n_vertices, 3) NumPy array of 3D vertex positions, where the i-th row gives the 3D position of the i-th vertex.
• F is a list of lists; each sublist represents a polygonal mesh face of arbitrary degree, using 0-indexed vertices.

Both compute_distance_to_mesh() functions take an optional argument called options, which is a dictionary with the following possible entries:

Field	Default value	Meaning
level_set_constraint	"ZeroSet"	Whether to apply level set constraints, with options “ZeroSet”, “None”, “Multiple”, corresponding to preservation of the input surface as the zero set, as multiple level sets (one for each surface component), or no constraints, respectively.
t_coef	1	Sets the time used for short-time heat flow. Generally you don’t have to change this.
bbox_min		The 3D position of the minimum corner of the computational domain, which is assumed to be an axis-aligned rectangular prism. If not specified, the size of the domain will be automatically computed so as to encompass the input source geometry.
bbox_max		The 3D position of the maximum corner of the computational domain.
resolution	np.array([2**5, 2**5, 2**5])	3D vector specifying the tet or grid spacing, with larger values indicating more refinement. If solving on a grid, this corresponds to the number of nodes along each dimension. Default values are $2^{5}$.
rebuild	True	If True, force (re)build the underlying tet mesh or grid domain. This will induce the solver to re-factorize the matrices involved in the solve.

Signed distance to point clouds

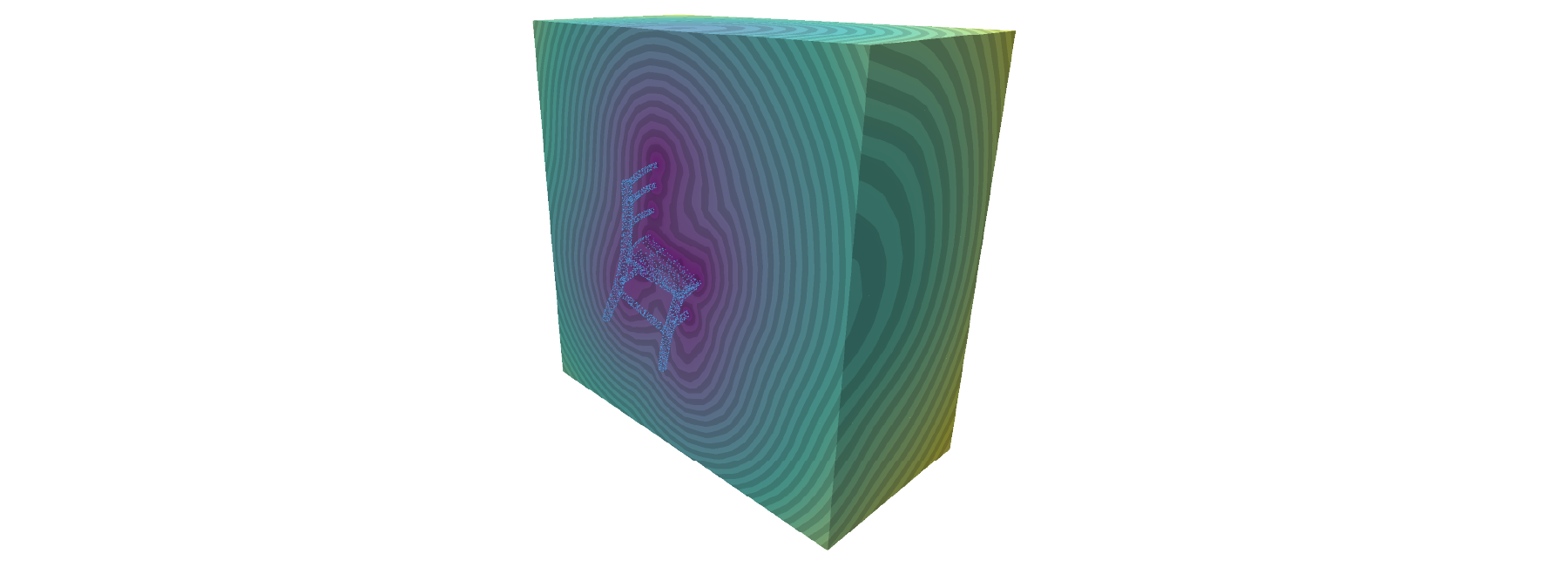
Example:

import signedheat3d as shm

P, N = # your point cloud, with normals

# Initalize tet mesh solver
tet_solver = shm.SignedHeatTetSolver(verbose=True) # print all messages

# Solve!
sdf_tets = tet_solver.compute_distance_to_point_cloud(P, N)

# Solve on a regular grid instead.
grid_solver = shm.SignedHeatGridSolver(verbose=True)
sdf_grid = grid_solver.compute_distance_to_point_cloud(P, N)

SignedHeatTetSolver.compute_distance_to_mesh(P: np.ndarray, N: np.ndarray, options: dict = {}) -> np.ndarray

Solve for an SDF on a tet mesh, to the point cloud represented by the point positions array P and point normals N.

• P is a (n_points, 3) NumPy array of 3D point positions, where the i-th row gives the 3D position of the i-th point.
• N is a (n_points, 3) NumPy array of 3D normal vectors, where |P| = number of points in the source point cloud.

SignedHeatGridSolver.compute_distance_to_mesh(P: np.ndarray, N: np.ndarray, options: dict = {}) -> np.ndarray

Solve for an SDF on a grid, to the point cloud represented by the point positions array P and point normals N.

• P is a (n_points, 3) NumPy array of 3D point positions, where the i-th row gives the 3D position of the i-th point.
• N is a (n_points, 3) NumPy array of 3D normal vectors, where |P| = number of points in the source point cloud.

Both compute_distance_to_mesh() functions take an optional argument called options, which is a dictionary with the following possible entries:

Field	Default value	Meaning
t_coef	1	Sets the time used for short-time heat flow. Generally you don’t have to change this.
bbox_min		The 3D position of the minimum corner of the computational domain, which is assumed to be an axis-aligned rectangular prism. If not specified, the size of the domain will be automatically computed so as to encompass the input source geometry.
bbox_max		The 3D position of the maximum corner of the computational domain.
resolution	np.array([2**5, 2**5, 2**5])	3D vector specifying the tet or grid spacing, with larger values indicating more refinement. If solving on a grid, this corresponds to the number of nodes along each dimension. Default values are $2^{5}$.
rebuild	True	If True, (re)build the underlying tet mesh or grid domain. This will induce the solver to re-factorize the matrices involved in the solve.

Helper functions

Tet mesh solver

SignedHeatTetSolver.get_vertices() -> np.ndarray

Returns an (n_vertices, 3) NumPy array representing the vertex locations of the underlying tet mesh domain.

SignedHeatTetSolver.get_tets() -> np.ndarray

Returns an (n_tets, 4) NumPy array representing the tetrahedra of the underlying tet mesh domain, where each tetrahedra is given by four vertex indices (0-indexed).

SignedHeatTetSolver.isosurface(f: np.ndarray, isovalue: float = 0.) -> tuple[np.ndarray, list[list[int]]]

Contours a scalar function defined on the tet mesh, given by the input vector f, according to the isovalue isovalue. Returns the tuple (vertices, faces) defining the polygon mesh of the resulting isosurface.

Grid solver

SignedHeatGridSolver.get_grid_resolution() -> list[int]

Returns a length-3 array giving the number of cells of the background grid along the x-, y-, and z-axes, respectively.

SignedHeatGridSolver.get_bbox() -> tuple[np.ndarray, np.ndarray]

Returns the tuple (bbox_min, bbox_min), where bbox_min and bbox_min are the 3D positions of the minimal and maximal node corners of the grid, respectively.

SignedHeatGridSolver.to_grid_array(f: np.ndarray) -> np.ndarray

Converts the input vector f representing a scalar function on the background grid, into a NumPy array of shape (dim_x, dim_y, dim_z), where dim_[xyz] gives the number of grid nodes along each axis.