A Heat Method for Generalized Signed Distance
ACM Transactions On Graphics (SIGGRAPH 2024)

Abstract
We introduce a method for approximating the signed distance function (SDF) of geometry corrupted by holes, noise, or self-intersections. The method implicitly defines a completed version of the shape, rather than explicitly repairing the given input. Our starting point is a modified version of the heat method for geodesic distance, which diffuses normal vectors rather than a scalar distribution. This formulation provides robustness akin to generalized winding numbers (GWN), but provides distance function rather than just an inside/outside classification. Our formulation also offers several features not common to classic distance algorithms, such as the ability to simultaneously fit multiple level sets, a notion of distance for geometry that does not topologically bound any region, and the ability to mix and match signed and unsigned distance. The method can be applied in any dimension and to any spatial discretization, including triangle meshes, tet meshes, point clouds, polygonal meshes, voxelized surfaces, and regular grids. We evaluate the method on several challenging examples, implementing normal offsets and other morphological operations directly on imperfect curve and surface data. In many cases we also obtain an inside/outside classification dramatically more robust than the one obtained provided by GWN.


- C++ geometry-central implementation. (2D surfaces) Applies on triangle mesh, polygon mesh, and point cloud domains.
- C++ implementation for 3D volumetric domains & demo project. Computes SDFs to point clouds, triangle meshes, and polygon meshes in 3D.
- Python (bindings to C++ code for 2D domains) Applies on triangle mesh, polygon mesh, and point cloud domains.
- Python (bindings to C++ code for 3D domains) Computes SDFs to point clouds, triangle meshes, and polygon meshes in 3D.
- Demo project (C++, 2D surface domains)
- Demo project (C++, 3D)
Acknowledgements
This work was funded by an NSF CAREER Award (IIS 1943123), NSF Award IIS 221229, a Packard Fellowship, and gifts from Adobe Research. The authors also thank Alec Jacobson for helpful conversations about winding numbers and the pseudonormal.Fast Forward
Talk at SIGGRAPH 2024
What is this paper about?
The signed distance function (SDF) of a shape \(\Omega\), evaluated at a query point \(x\), returns a value whose magnitude is the distance from \(x\) to the closest point on \(\Omega\), and whose sign indicates whether \(x\) is inside or outside \(\Omega\):
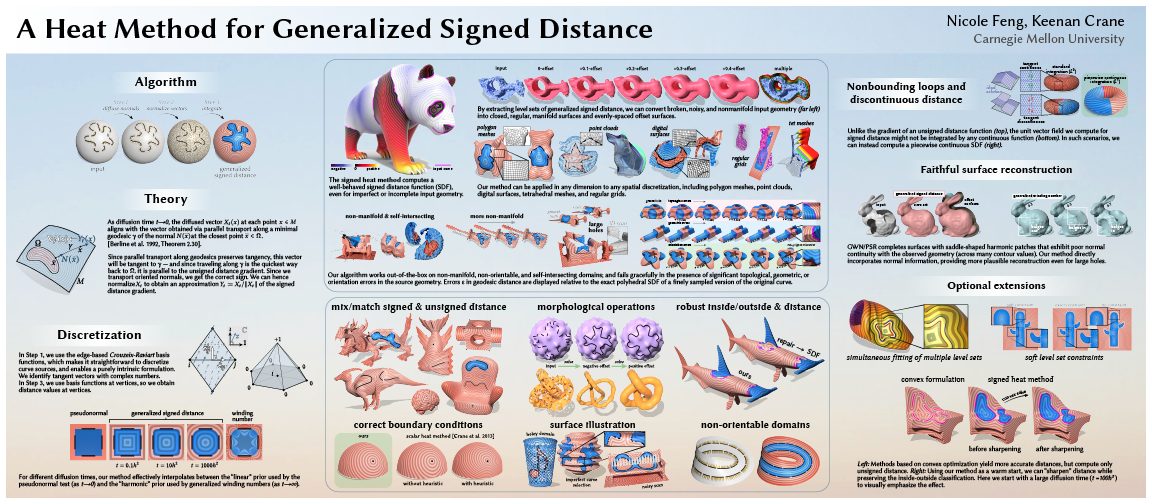
 An SDF (visualized with isolines) of curves on a 2D surface (left), and an SDF of a 2D surface in 3D space (right).
An SDF (visualized with isolines) of curves on a 2D surface (left), and an SDF of a 2D surface in 3D space (right).
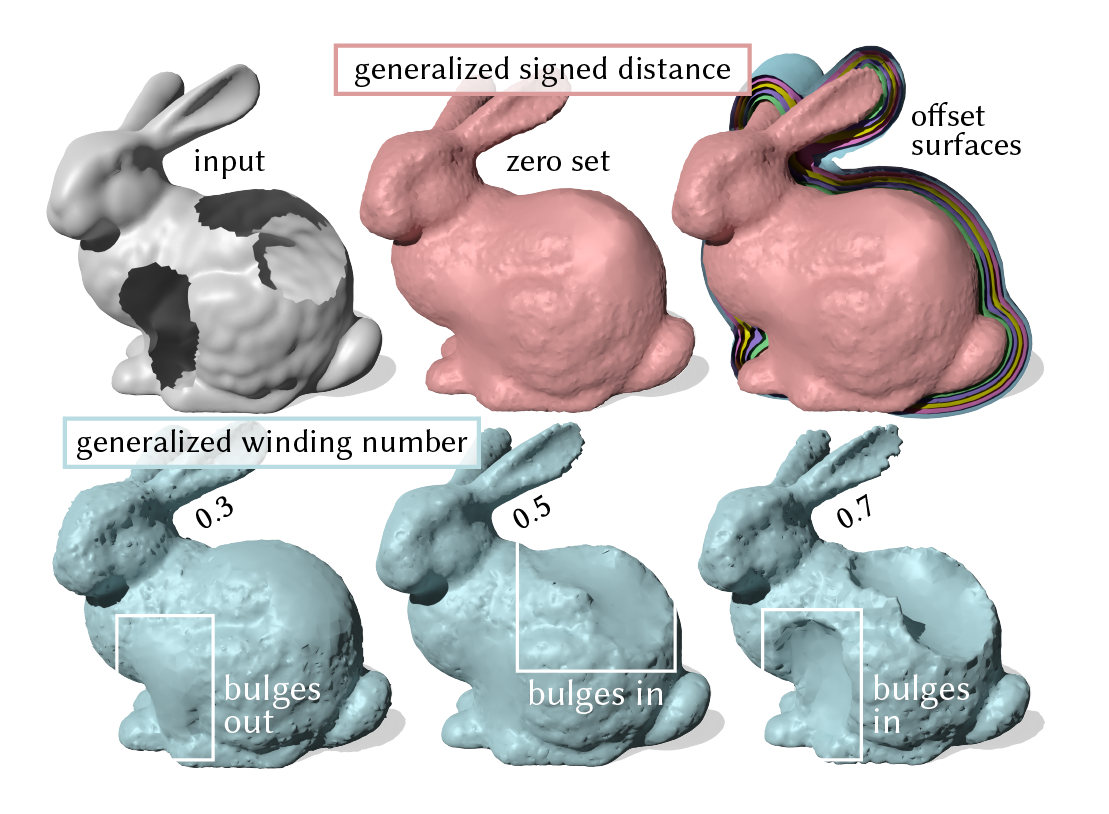
SDFs form an essential building block of many algorithms across graphics, geometry processing, vision, robotics, and more. However, the meaning of "inside"/"outside" — and hence signed distance — is not well-defined whenever the source geometry \(\Omega\) is "broken", meaning \(\Omega\) might have holes, self-intersections, noise, or other errors.
So we introduce the Signed Heat Method (SHM) for computing signed distance to broken geometry. The generalized signed distance functions computed by our method are robust across a wide variety of errors in the input, and generalize signed distance to cases not previously considered by past distance algorithms. Our method in principle applies to all discretizations and all dimensions, and we show many such examples in the paper:
 An overview of what our method can do. Scroll down (or read the paper) for more examples!
An overview of what our method can do. Scroll down (or read the paper) for more examples!
Our algorithm is simple and efficient, consisting of three basic steps. First we diffuse the normals of the source geometry \(\Omega\), which extends information about the \(\Omega\)'s orientation to the rest of the domain \(M\). Then we normalize the diffused vectors, yielding a unit vector field that approximates the gradient of an SDF. Finally, we find the function whose gradient best matches this unit vector field, obtaining our generalized SDF.

Our algorithm makes use of the remarkable fact that parallel transport along shortest geodesics (shortest paths) can be computed using short-time vector diffusion [Berline et al. 1992, Thm. 2.30]. We aren’t the first to make use of this fact in geometry processing — that would be The Vector Heat Method by Sharp et al. 2019 — but we recognized its implications for computing signed distance. In particular, the theorem guarantees that for small diffusion time, diffused normal vectors of \(\Omega\) will be parallel to the gradient of signed distance (essentially reproducing a well-known property of SDFs that the gradient at a point \(x\) is equal to the normal at the point on \(\Omega\) closest to \(x\).) Then, because we know diffused normals will point in the same direction as the gradient, we can normalize and integrate these vectors to recover an accurate SDF. Our algorithm boils down to solving two sparse linear systems: a (screened) Poisson problem to diffuse normal vectors, and another Poisson problem to integrate the resulting vector field.
Some results
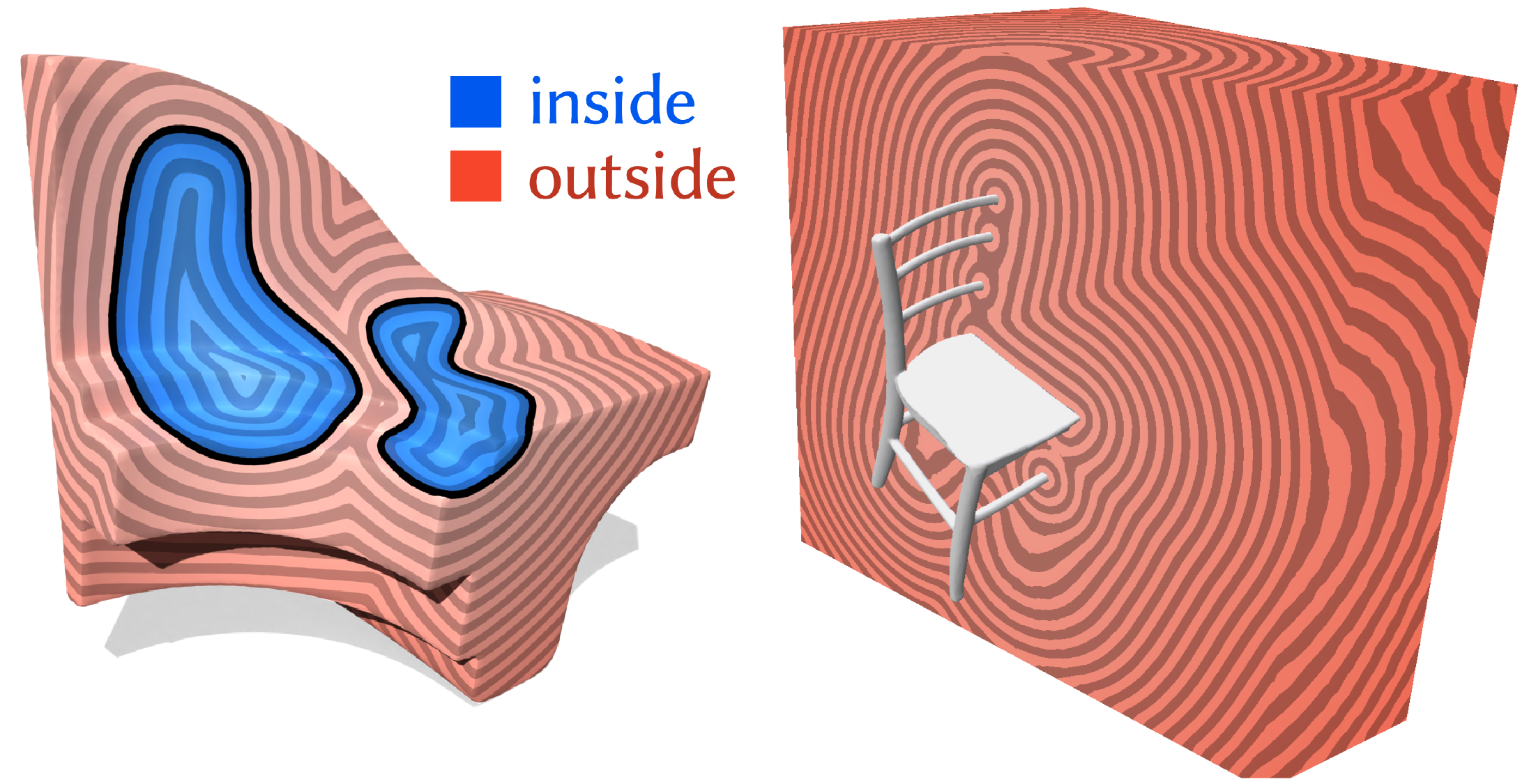
Our method is robust on broken geometry, because diffusion effectively interpolates normals from nearby points, and extends limited information about orientation to the rest of the domain. Because our method is based purely on PDEs, it generalizes to curved surfaces, different spatial discretizations, and allows one to easily incorporate constraints. Our particular discretization (using edge-based functions to encode vector fields) enables a purely intrinsic formulation, allowing for additional robustness via intrinsic Delaunay refinement; it also lets the method apply directly to non-manifold and self-intersecting meshes.
We show that our method is robust to defects in the source geometry...
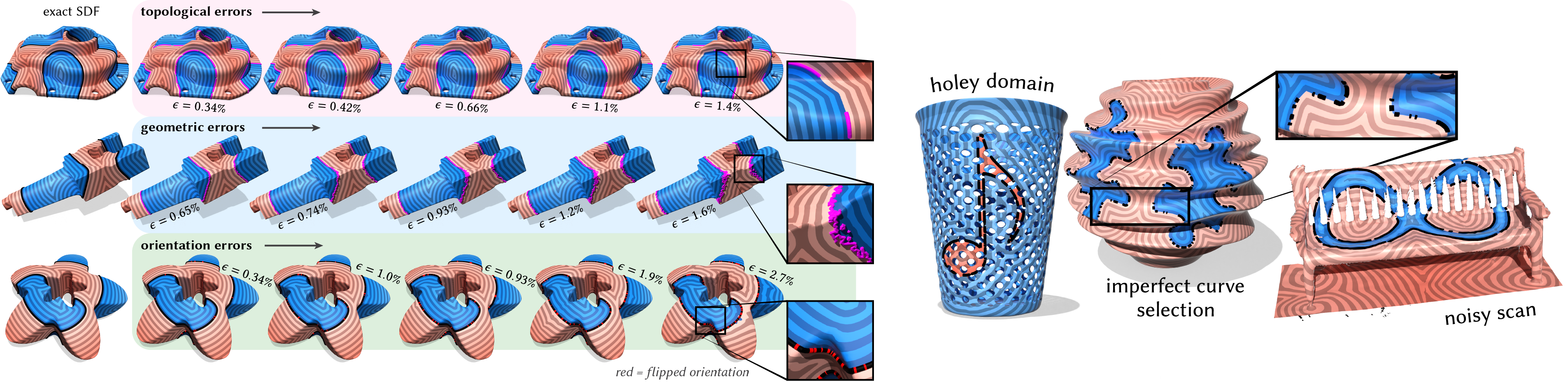
...as well as to errors in the domain:
Our method works on non-orientable surfaces:

We show results on a variety of surface discretizations beyond triangle meshes:

And also a variety of volumetric discretizations:

With generalized signed distance established as a basic tool, like generalized morphological operations that can simplify high-frequency features of broken shapes as if they were whole ("dilation"/"erosion"):
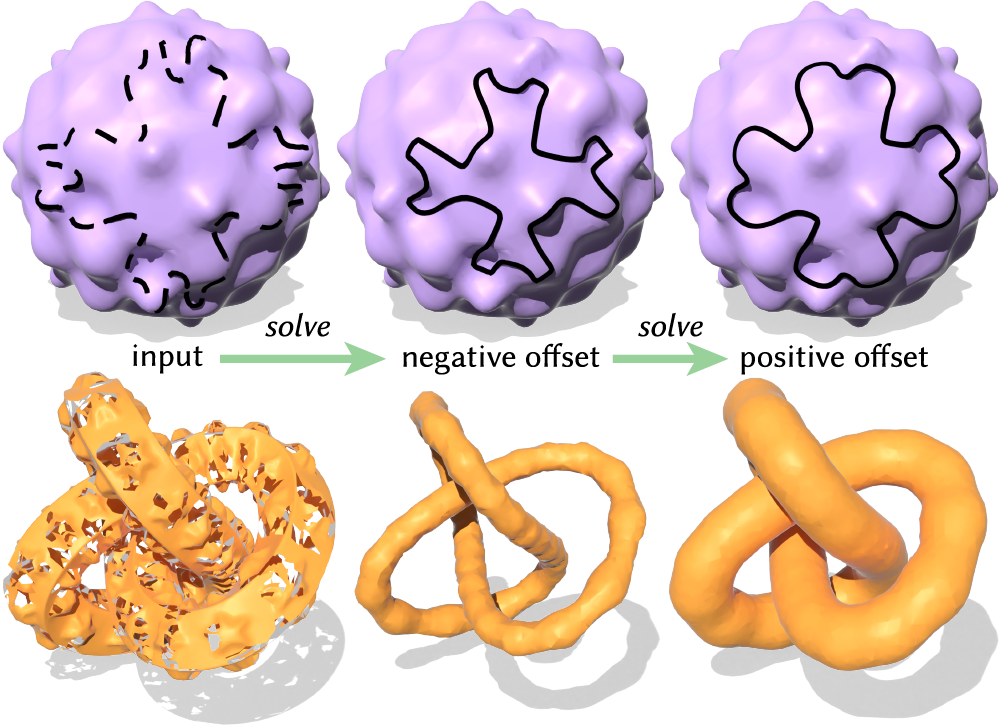
In addition to generalized signed distance, our method can compute unsigned distance to curves and point sources, subsuming past heat methods. We can compute distance fields that combine all of these types of distance:

We also show that the SHM is more accurate than past heat methods while having the same asymptotic cost, while being an order of magnitude faster than other state-of-the-art algorithms for geodesic distance [Belyaev & Fayolle 2020].
Errata
The right-most image in Figure 8, which compared the boundary conditions of our method to the boundary condition heuristic of the unsigned heat method (UHM), was incorrect: I made a mistake in applying the paper's suggested boundary conditions, and in fact the UHM can yield an unsigned distance field whose behavior at the boundary is comparable to ours. The correct figure should be
Compared to the original figure, only the right-most image is changed ("unsigned heat method with heuristic"). Unfortunately I can't update the ACM-published version of our paper, but the paper PDF linked on this website, and all presentation materials, have been updated with the correct information. Sorry! I regret any confusion I caused about heat diffusion and its behavior.
Discussion
Vector diffusion \(\rightarrow\) effective surface reconstruction
While we began this project with signed distance in mind, we found that vector diffusion also yields more faithful surface reconstruction than winding numbers/Poisson Surface Reconstruction (which essentially use scalar diffusion). The latter methods fill in holes with flat or saddle-like patches, behavior which is endemic to their underlying PDE and thus independent of the observed surface. In contrast, vector diffusion interpolates observed normal vectors, so we fill in holes with patches that more closely align with the curvature of the surrounding surfaces:
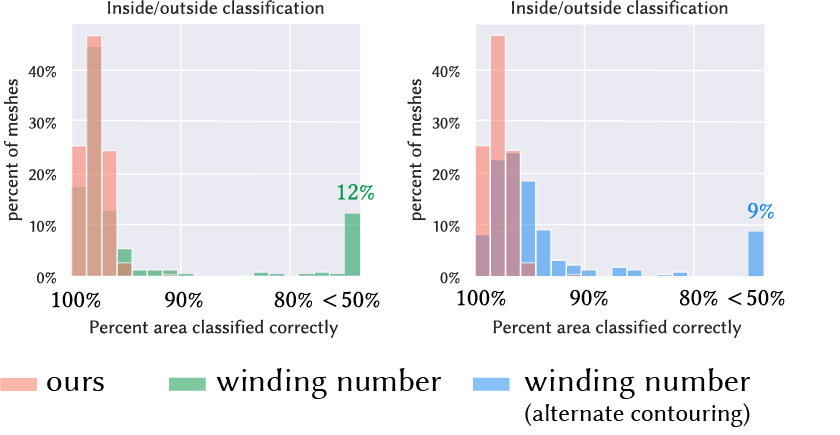
Our experiments were also a reminder that contouring winding number is really difficult. Regardless of what contouring strategy we tried, there were inevitably a significant number of cases on our benchmark where contouring failed miserably at classifiying inside/outside. Here's an example comparing the generalized signed distance function produced by our method, vs. contouring first using winding number, then computing distance to the contoured curve:

Contouring has been a noted Achilles' heel for winding number since its introduction to graphics; Jacobson et al. 2013 ("Robust Inside-Outside Segmentation using Generalized Winding Numbers", Section 5) had noted that simply contouring according to the 0.5 levelset is often insufficient and proposed a graph cut optimization, though it isn't clear the latter is any better (it isn't implemented in the official release in libigl).
I had also encountered the challenges of contouring winding number during our previous surface winding numbers project, where I had developed a contouring procedure that at least worked better than previous methods. Still, our experiments show that contouring winding numbers is far from "automatic". In this project, I ended up trying two methods for contouring winding number functions on surfaces: (1) the method from our surface winding numbers paper, and (2) contouring according to the average function value along one side of the curve. Both methods yield pretty inconsistent inside/outside classification on a benchmark of 220 examples, where both methods failed terribly on ~10% of examples (where "terrible" = more than 50% of surface area was misclassified):
"Small" things
Our algorithm is purely intrinsic for curved surface domains, which is not only satisfying in the sense that we've placed minimal assumptions on our input geometry, but also because it allows us to use the machinery of intrinsic triangulations to robustify PDE solves if necessary. In particular, the first step of our algorithm uses edge-based operators that makes discretizing the source term is particularly easy: we don't have to worry about mapping from the tangent space of the triangle face of a curve segment, to, say, the tangent space of a vertex. Instead we can do everything neatly using a single face, using only intrinsic operations.
For the least-squares optimization \(\min_{\phi:\ M\to\mathbb{R}} \int_M \|\nabla\phi-Y_t\|^2\) in Step 3, our paper states the Euler-Lagrange equations with boundary conditions (Equation 3). Then careful discretization of divergence, again taking into account the domain boundary, yields an "extra" boundary term due to Stokes' theorem — that happens to exactly cancel out these boundary conditions. The unsigned heat method paper implicitly relied on these boundary conditions, but I didn't understand what they were from reading the paper, so it was satisfying for me to finally understand why this was the case. Perhaps these things were obvious to geometry processing veterans, but they weren't obvious to me at first.
Finally, deriving the representation of point sources involved taking the limit as the radius \(\varepsilon\) of a geodesic circle goes to 0. Luckily, a similar derivation was already done in Appendix A of The Vector Heat Method. However, their derivation is equivalent to taking the limit as \(\varepsilon\to 1\) instead of \(\varepsilon\to 0\). If we were to take \(\varepsilon\to 0\) in their derivation, we would actually get zero: vertex-based functions don't have enough degrees of freedom to represent a radially-symmetric vector field concentrated at a single vertex. Taking \(\varepsilon\to 1\) effectively "spread out" the support of the source term to nearby vertices. Our derivation is properly scale-invariant, in addition to working in practice.
Some side quests
To implement this project, I ended up implementing the complex-valued Crouzeix-Raviart connection Laplacian on triangle meshes, polygon Laplacians, and barycentric vectors. These features are now implemented in geometry-central, in addition to the signed heat method itself.
For polygon Laplacians, there had been two recent papers with different constructions ("Discrete differential operators on polygonal meshes" by De Goes et al. 2020, and "Polygon Laplacian Made Simple" by Bunge et al. 2020) and I wasn't sure of their respective advantages, so I just implemented both.Open questions
Crouzeix-Raviart behavior
The first step of our method involves solving a discrete Poisson question with a particular source term. Following the "standard" finite element procedure, we represent this source term in a particular basis, which in our case involves integrating this source term against (vector) Crouzeix-Raviart basis functions. This leads to an expression weighted by a scalar Crouzeix-Raviart basis function, though in practice we found that we obtained more accurate results by omitting this scaling factor. Could it be that since Crouzeix-Raviart functions are non-conforming, that our approach yields the correct behavior by using piecewise constant vector bases (instead of piecewise linear)? It's not entirely clear to me what's going on from a function space perspective.
Graph distance as \(t\to 0\)?
Similar to the unsigned heat method, we observe empirically that the unsigned distance produced by our method behaves like graph distance as \(t\to 0\):
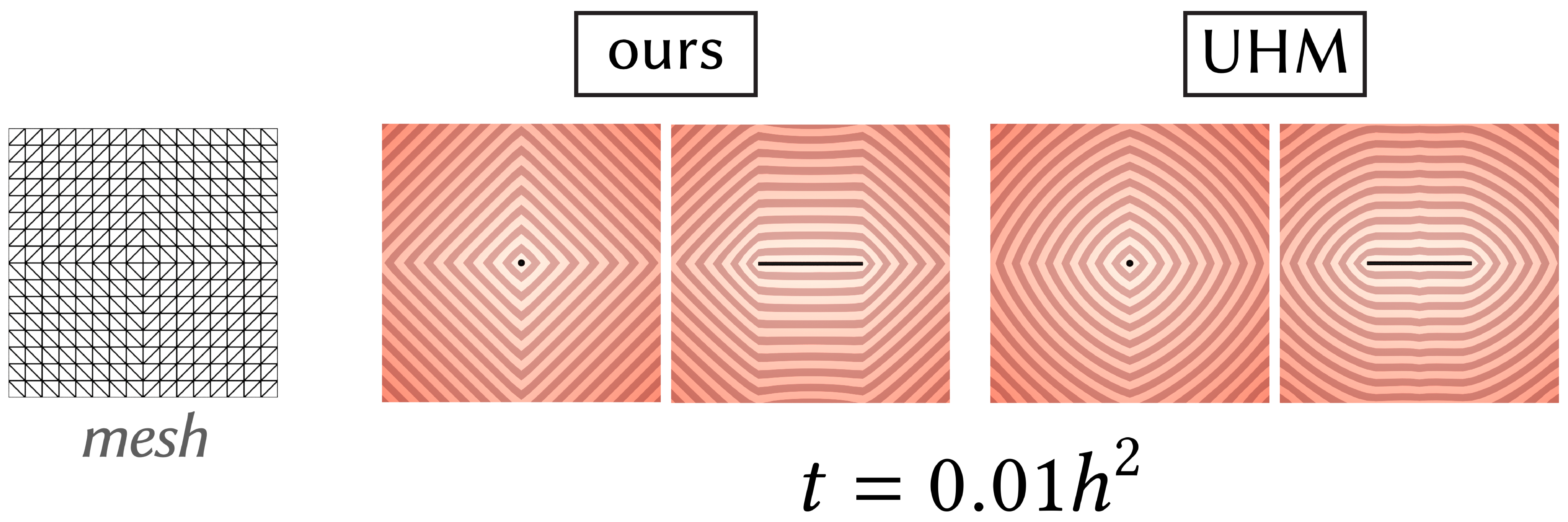
However, it's not immediately clear to me why. Crane et al.'s proof (Crane et al., Appendix A) relies on Varadhan's formula involving scalar heat flow, whereas our method depends on vector heat flow. Given some time, I'd like to derive a similar proof using the relevant asymptotic relationships.
Finer-grained control of surface completion
The accuracy of our signed distance gradient approximation relies on the asymptotic behavior of the vector heat kernel as \(t\to 0\). Hence our completions tend to be more pseudonormal-like (corresponding to \(t\to 0\)) rather than winding number (corresponding to \(t\to \infty\)). You can get more "harmonic" fills by increasing the diffusion time, but this tends to make the distance approximation worse. Question: How to get the best of both regimes?

